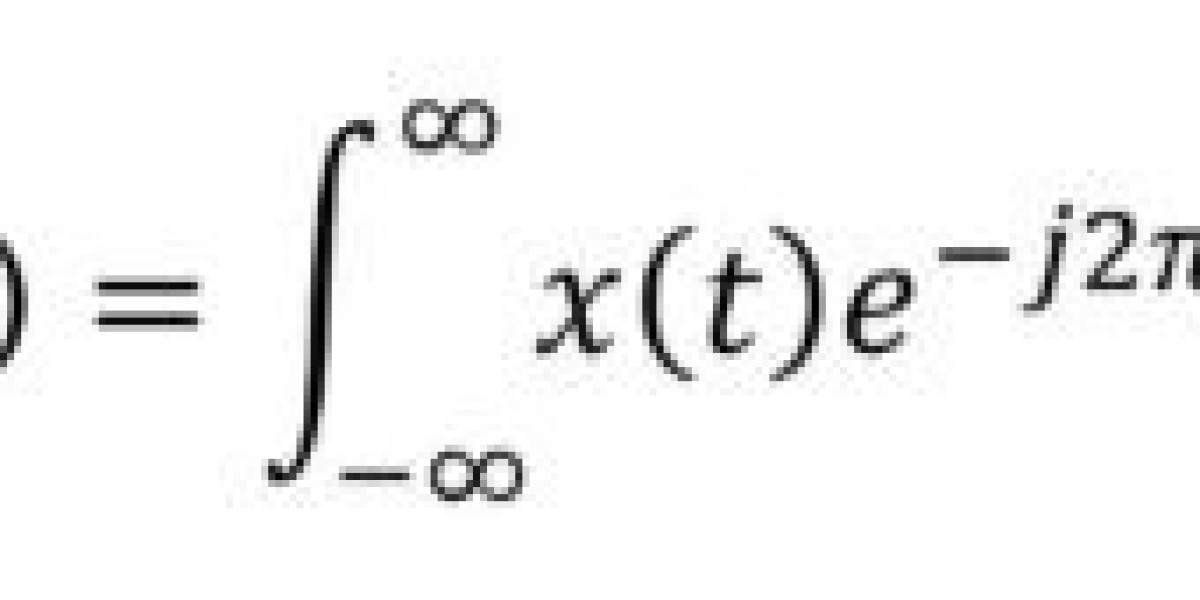An Overview and Its Applications

Undoubtedly, the Fourier Transform is one of the most powerful features in mathematics, engineering, and even in physics. Looking at the equation might leave you awestruck by its depth and complexity. This is exactly the reason why we are here. This post seeks to unravel the Fourier transform, its foundational theorem, and how it changes the signal and data analytics game. The forth coming sections will dissect the advantages that come with the Fourier Transform.

What is Fourier Transform?

The Fourier Transform by definition is a mathematical tool that splits a signal (which can be a function of space, time and frequency) into its basic constituents or isolated individual frequencies. Try to imagine the reduce function to take a musical piece and divide it into its component notes, each of which is defined by a certain frequency, amplitude, and phase.

This incredible math technique alters the form of time signals (such as audio) to convert them into sounds. This method exposes various patterns, behavioral insights, and intricacies that span many fields: audio engineering, medical imaging (like MRIs), and telecommunications.

Theorem 4.

Suppose that F(t) is piecewise smooth on every bounded interval and that [latex]\int _{-\infty }^{\infty }\left|F\left(tight)dtight|[/latex] exists. Then the Fourier transform, [latex]G\left(\omega ight)[/latex], of F exists and

[latex]p.v\ \int _{-\infty }^{\infty }G\left(\omega ight)e^{i\omega t}d\omega =\ \begin{cases}F\left(tight)&\ where\ F\ is\ continuous\\
\frac{F\left(t+ight)+F\left(t-ight)}{2}&\ \ otherwise.\end{cases}[/latex

Example 1

Find the Fourier transform and verify the inversion formula for the function
[latex]F\left(tight)=\frac{1}{t^2+4}.[/latex]

Solution.

Observe that

[latex]F\left(tight)=\frac{1}{t^2+4}=\frac{1}{\left(t-2iight)\left(t+2iight)}.[/latex]

is analytic except for simple poles at  t= ±2. We shall use residue theory to evaluate the Fourier transform, interpreting the integral as a principal value:

[latex]G\left(\omega ight)=\frac{1}{2\pi }p.v\int _{-\infty }^{\infty }\frac{e^{-i\omega t}}{t^2+4}dt.[/latex]

If [latex]\omega > 0[/latex], we close the contour with expanding semicircles in the lower half-plane; we find

[latex]\ G\left(\omega ight)=\frac{1}{2\pi }\left(-2\pi iight)Res\left(\frac{e^{-i\omega t}}{t^2+4};\ -2iight)[/latex]

[latex]G\left(\omega ight)=-i.\ \lim _{t\to -2i}\ \frac{e^{-i\omega t}}{t-2i}=\frac{e^{-2\omega }}{4\ }\ \ \ \ \ \ \left(\omega \ge 0ight).[/latex]

Similarly, for [latex]\omega <0[/latex] we close in the upper half-plane and find
[latex]G\left(\omega ight)=\frac{1}{2\pi }\left(2\pi iight)Res\left(\frac{e^{-i\omega t}}{t^2+4};\ -2iight)=\frac{e^{2\omega }}{4\ }\ \ \ \ \ \ \ \ \ \ \ \ \ \ \left(\omega <0ight)[/latex]
In short

[latex]G\left(\omega ight)=\frac{e^{-2\left|\omega ight|}}{4}[/latex].

To verify the Fourier inversion formula we compute

[latex]\int _{-\infty }^{\infty }G\left(\omega ight)e^{i\omega t}d\omega =\int _{-\infty }^{\infty }\frac{e^{-2\left|\omega ight|}}{4}e^{i\omega t}d\omega .[/latex]

By symmetry, the imaginary part vanishes, and this integral equals

[latex]Re\int _{-\infty }^{\infty }\frac{e^{-2\left|\omega ight|}}{4}e^{i\omega t}d\omega =2.Re\ \int _0^{\infty }\frac{e^{-2\omega }}{4}.e^{i\omega t}d\omega .[/latex]

[latex]=\frac{1}{2}Re\ \left|\frac{e^{\left(-2+itight)\omega }}{-2+it}ight|_{\omega =0}^{\infty }=\frac{1}{t^2+4}.[/latex]

Hence

[latex]\frac{1}{t^2+4}=\int _{-\infty }^{\infty }\frac{e^{-2\left|\omega ight|}}{4}e^{i\omega t}d\omega [/latex]

As is the case of Fourier series, a wealth of theorems has been discovered stating conditions under which the Fourier integral representations (7) and (8) are valid. A useful one for applications deals with piecewise smooth functions F(t) ; that is, on every bounded interval F(t) is continuously differentiable for all but the finite number of values[latex]t=\tau _1,\tau _2,\tau _3,...,\tau _n[/latex]  and at each [latex]\tau _j[/latex] the "one-sided limits" of F(t) and F'(t) exist. Note the principal value interpretation of the integral is called for in the theorem; this ensures that the inverse transform converges at the points of discontinuity.

Why the Fourier Transform Is Important 

To appreciate the Fourier transform deeply, you must comprehend its scope within the global context. Consider the following: 

1. Audio Processing: While audio engineers work on sound editing, they utilize the Fourier Transform to eliminate unnecessary background noise and enhance specific frequencies for corresponding sounds.

2. Image Compression: Transformation and Loading Interchange Format JPEG uses more Fourier compression for images compared to other visuals.

3. Quantum Physics: Analyzing wave functions in quantum mechanics would have been very hard without The Fourier Transform.

4. Medical Imaging: MRI and CT scans depend so heavily on this Transform that devising new approaches to these imaging modalities without it would be unproductive.

Every leading-edge technology that dominates everyday life could not depend on this tool. 

The Fundamental Theorem of Fourier Transform 

The Fourier transform has a magic bound whenever arithmetic is powerful with mathematical an integer region concept, as for magic item lies their core theorem: 

Every periodic signal or function is formed aligning differently rotated sine and cosine sum waves distributed differingly thematically signals/concept frequency domain signals of varying amplitude and phases frequencies.

Let's explain it step by step: 

• Reacting operations over a given period can be expressed as a sum of sinusoidal waves.
• The concept can be extended to include signals, sound waves, light waves, and even stock market prices!

Here is the equation that explains everything in the differential form: 

Continuous the Fourier transform Formula 

\[ F(f) = \int_{-\infty}^{\infty} x(t) \cdot e^{-i 2 \pi f t} \, dt \]  

Where: 

• The frequency spectrum of the original function is given by \( F(f) \).
• A signal defined in the domain of time is given by \( x(t) \).
• Components of the sine and cosine wave are given by \( e^{-i 2 \pi f t} \).
• Continuous integration is also defined by \( dt \) Whats ever it represents.

At first glance the formula above might look intimidating, think about it in this particular way - you have numerous sine and cosine waves. You need to realize in your signal for each one how much energy is available. 

The Key Types of Fourier Transform 

There are various forms of the Fourier transform depending on the nature of the data being analyzed or worked on: 

1. Continuous Fourier Transform - Suitable for ongoing signals and is perfect for most theoretical models.
2. Discrete Fourier Transform (DFT) - This is made for use with computers and relates to digital data, breaking up the signals into finite pieces.

3.FFT (Fast Fourier Transform) – An algorithm that calculates the DFT phenomenally fast. It is used in most real-time systems.

Fourier Series and Fourier Transform

There are two important differences between the Fourier Transform and the Fourier Series that should be noted:

• The Fourier Series concerns itself with periodic signals (or repeating waveforms) like clock signals.
• The Fourier Transform can work with both periodic and non-periodic aperiodic signals.

Application of the Fourier Transform in Real Life

1. Audio Track Analysis

Do you remember the time you adjusted the equalizer on your music player? It modifies specific frequencies and boosts bass, treble, or even vocals. That’s the Fourier Transform separating the music into its frequency constituents for polishing.

2. Medical Imaging

MRI scanners pulse the body with radio waves and register the radio waves that come back out. The received waves are transformed using the Fourier Transform to build detailed images of different sections of the body.

3. Telecommunications

Wi-Fi, radio signals, and 5G are all modern methods of communication which require splitting a signal into frequency channels. The Fourier Transform facilitates dividing the signal by frequency components and modulating the signal using its frequency.

4. Geophysics

Seismologists apply the Fourier Transform to seismic data with the objective of determining the frequency content of the earthquakes and in some cases generating aftershock predictions.

Demonstrating the Fourier Transform

At times, appreciating a concept as it is presented is beneficial. Visualize the following scenario:

1. A time-domain signal is graph depicting a curve that moves like a wave, akin to an audio waveform.
2. When a Fourier Transform is executed, a bar graph is produced. A frequency spectrum with the most prominent frequencies and their amplitudes is depicted.

This graphic aids to illustrate which portions of a signal include the majority of information, making it easier for the next step of signal analysis and improvement.

Drawbacks of the Fourier Transform

However, as powerful as it is, a Fourier transform still has weaknesses such:

1. Time-Frequency Constraint: It has no means of specifying when certain frequencies occur within a particular time period, which can be solved using the Short-Time Fourier Transform (STFT) or Wavelet Transform.
2. Processing for larger signals could be expensive, though measures such as FFT have solved this problem to some degree.

For Feature Extraction using Fourier Transform

Anyone working with signals or data or even waveforms must certainly know about the Fourier Transform. Software such as MATLAB or SciPy in Python make Fourier analysis accessible to anyone even without much requisite math knowledge.

Transform The World

Audio processing, medical image analysis, and stock market analysis all draw upon the theory and application of the Fourier Transform. It appears to be a complicated mathematical tool, but its use should be harnessed by almost all industries that deal with data signals. Learning the basics and technologies that support it makes it easier for the Fourier Transform to be a revolutionizing tool in one’s career or industry. The only limitation is the willingness to explore its potential.